网络流入门

网络流基础概念

● 有向图：

由顶点和有向边构成的图，边具有方向。

● 容量：

在网络流中，每条边都有一个容量，代表该边能承载的最大流量。

● 流量：

实际通过边的流的数量，流量不能超过容量，且需满足流量守恒，即除源点和汇点外，每个顶点的流入流量等于流出流量。

● 源点和汇点：

源点是流的起点，只有流出的流；汇点是流的终点，只有流入的流。

网络流问题类型

● 最大流问题：

目标是找到从源点到汇点的最大可行流量。

● 最小费用流问题：

在满足流量要求的同时，使流的费用最小。

最大流算法思路

● Ford-Fulkerson算法：从初始的零流开始，不断寻找从源点到汇点的增广路径，即还有剩余容量的路径，沿着增广路径增加流量，直到找不到增广路径为止，此时得到的流就是最大流。

C++代码示例（Ford-Fulkerson算法）

(ps：写了好久的代码，结果全没了，气死我了。只能写在dev上，然后发图片了)

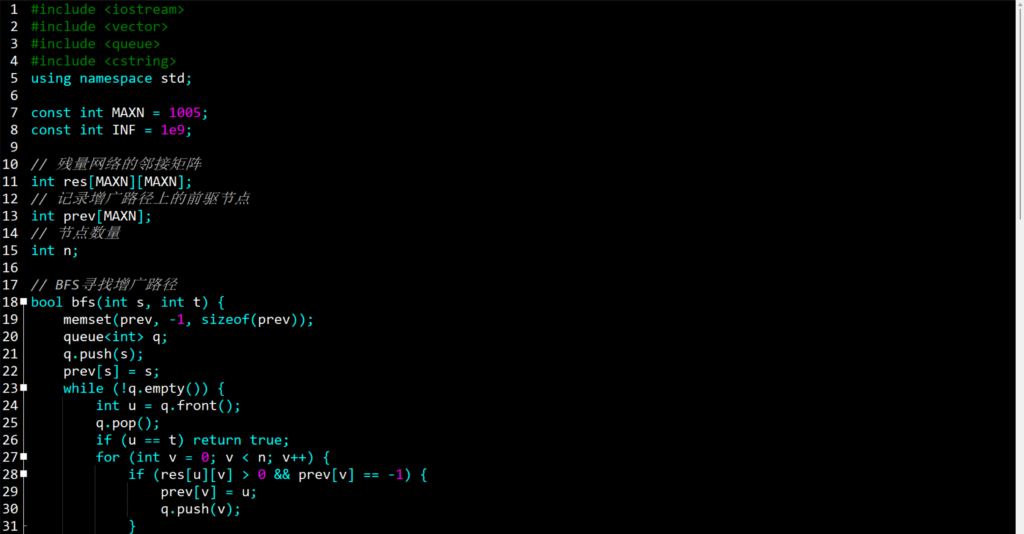
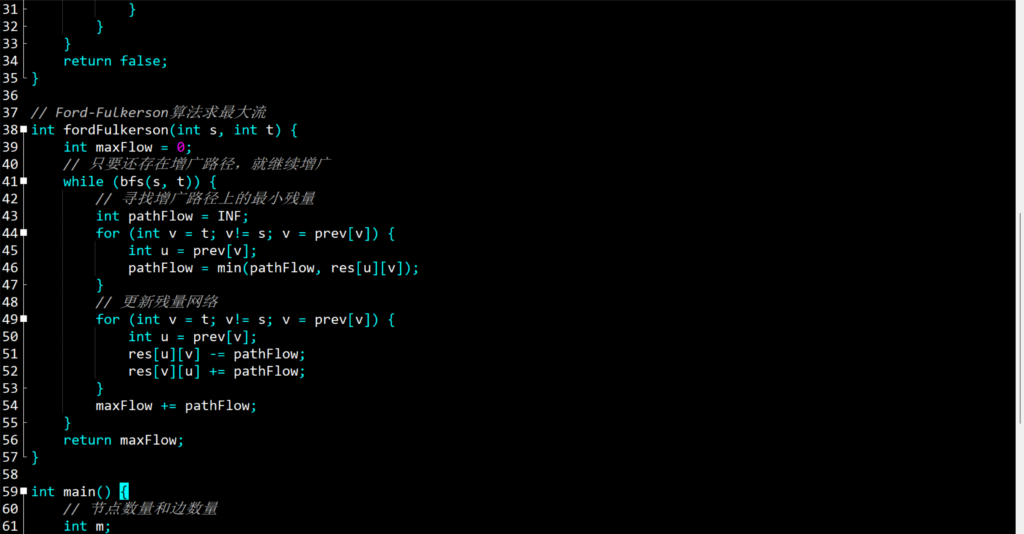
上述代码，fordFulkerson实现了Ford-Fulkerson算法最大流。

以上内容全部结束，谢谢大家的观看，也希望大家可以提出自己的疑问，指出文章中的错误之处，友善发言，

也希望我的文章可以给你带来一定的帮助谢谢大家！

引用一段金钩佬的AFO文章（完蛋，忘了是谁了）

“匆匆的时光从不等待，因为每个人都推着时代前行。 新一年的车轮缓缓而来，我们便不能滞留在原地。 有时候，竞赛就是这样残酷。它从不在乎你燃烧了几分青春，从不在乎你闯破了多少挫折，从不在乎你的热爱有多深多沉重，它只在乎，你能否击败所有对手。 包括那些孤注一掷的或蹉跎年华的人;包括那些资源比你多，起步比你早，视野比你宽，准备比你充分的人包括那些合群的或独行的人;包括那些自强的或失落的人;包括那些坚定的或踌躇的人;包括那些初露锋芒的或临近退役的人；包括那些为学位挣扎的或只为热爱的人;包括那些拼命挤时间却只为看OI一眼的人。 最终，真正走完全程，而被竞赛承认的获胜者，寥寥无几。但冰冷的凝视之下，正是热爱真正闪光之处。坚持和考验同样伟大。”

                                                                                                       ————Mozart.chen