博弈论入门

关键要素：

参与者：

• 参与博弈的各方，可以是个人、企业、国家等。

策略：

• 每个参与者在博弈中可以采取的行动方案。

收益：

• 参与者在不同策略组合下所获得的结果，通常用数值表示。

常见的博弈类型：

完全信息静态博弈：

• 参与者同时行动，且每个参与者都知道其他参与者的策略和收益。比如 “囚徒困境”，两个囚徒在不知道对方选择的情况下，决定是否坦白。如果两人都坦白，各判 8 年；如果一人坦白一人抵赖，坦白者释放，抵赖者判 10 年；如果两人都抵赖，各判 1 年。从整体最优来看，两人都抵赖是最好的结果，但从个人理性出发，两人都会选择坦白。

完全信息动态博弈：

• 参与者的行动有先后顺序，后行动者能观察到先行动者的行动。比如下棋，一方先走一步，另一方根据对方的走法再决定自己的走法。

不完全信息静态博弈：

• 参与者对其他参与者的策略和收益不完全了解。例如在拍卖中，竞拍者不知道其他竞拍者的心理价位。

不完全信息动态博弈：

• 参与者行动有先后顺序，且后行动者对先行动者的某些信息不完全了解。

1. 有两个玩家，双方轮流操作。

2. 游戏状态有限，且在有限步内结束。

3. 双方在任何时刻能采取的行动和行动规则相同，且与玩家无关。

4. 无法行动的玩家判负。

Nim 游戏：

1. 这是最为基础的博弈模型。有若干堆物品，每堆物品数量有限，玩家轮流从某一堆中取走任意数量物品（至少 1 个） ，最后取光物品的玩家获胜。其必胜策略判断依据是将每堆物品数量进行异或运算。若结果为 0，后行动者有必胜策略；若结果不为 0，先行动者有必胜策略。

• • 代码示例（C++）：（ps：又不能写代码了，只能用别的IDE然后截图了）

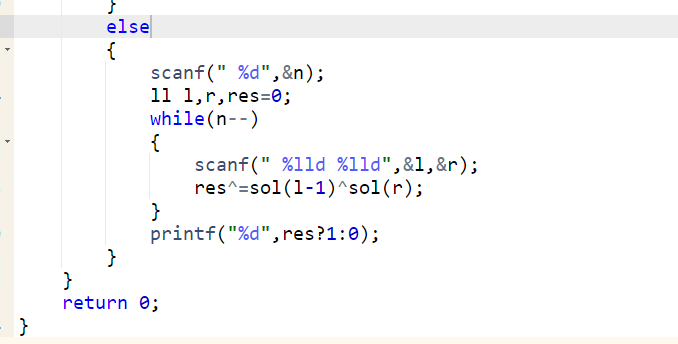
2. 巴什博弈（Bash Game）：只有一堆 n 个物品，两人轮流从这堆物品中取物，规定每次至少取 1 个，最多取 m 个。最后取光者得胜。若 ，则后取者有必胜策略；若 ，则先取者有必胜策略。先取者第一次取 个物品，之后每次取的物品数与后取者取的物品数之和为 ，这样先取者能保证取到最后一个物品。

• • 代码示例（C++）：
  • （不想写了 后续单独补上）

威佐夫博弈（Wythoff Game）：有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。设两堆物品数量分别为 a 和 b（ ），存在奇异局势 ，其中 ， （k = 0，1，2，...）。若当前局势是奇异局势，后取者有必胜策略；若不是奇异局势，先取者有必胜策略，先取者可以通过操作将局势变为奇异局势。

• • 代码示例（C++）：
  • (不想写了，后续单独补上)

1. 状态分析：首先要明确游戏的初始状态和终止状态，然后分析在不同状态下玩家的可行操作。例如在 Nim 游戏中，初始状态是各堆物品的数量，终止状态是所有物品被取光，玩家的可行操作是从某一堆中取走物品。

2. 寻找规律：通过对简单情况的分析，尝试找出博弈的规律。比如在巴什博弈中，对不同的 n 和 m 进行试验，就能总结出与 相关的必胜策略规律。

3. 利用数学工具：像 Nim 游戏中利用异或运算判断必胜策略，以及威佐夫博弈中利用黄金分割数等数学知识来确定奇异局势，都是借助数学工具解决博弈问题的体现。